Как да намерите квадратна зона, ако периметърът е известен, диагонал? Как да намерите квадрата на квадрата, вписан в кръга и описани близо до обиколката: формула, примери за решаване на проблеми. Как да намерите страната и диагонала на квадрата, ако е известна неговата площ?

Прочетете статията, за да знаете как да намерите квадратната зона по различни начини.

Съдържание

Квадрат е равностранен правоъгълник. Този правилен и плосък четириъгълник има равенство от всички страни, ъгли и диагонали. Поради факта, че има такова равенство, формулата за изчисляване на площта и други характеристики е леко модифицирана в сравнение с други математически фигури. Но това не прави задачите твърде сложни. Нека анализираме всички формули и решения на тази статия.

Как да намеря страната на площада, познавайки нейната зона?

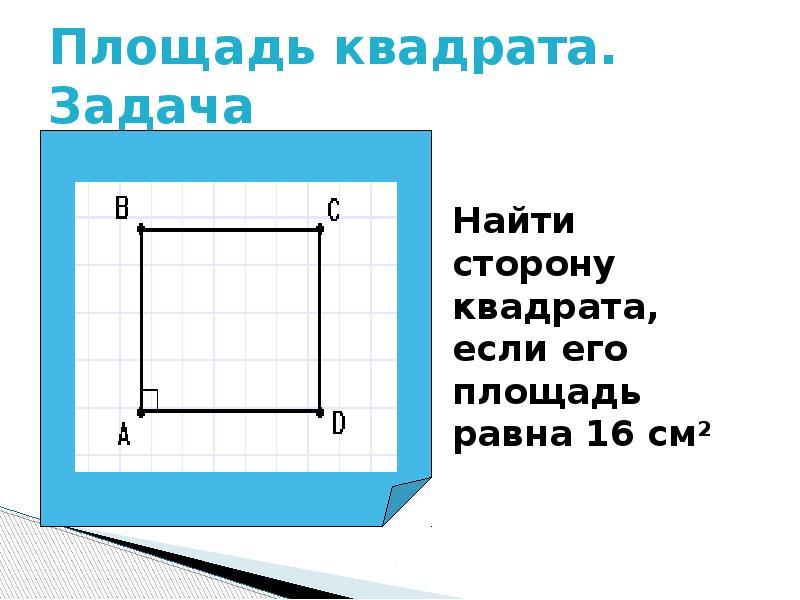
Квадрат С. Директните и квадратни квадратчета се изчисляват по формулата: a Умножете по б.. Но тъй като площадът има пълно равенство на страните, неговата площ ще бъде равна: S \u003d (a) във втора степен.Как да разберете размера на страната на площада, знаейки нейната площ?

Ако е известна площта на квадратния квадрат, тогава намираме страната, като изчисляваме площта изпод квадратния корен.
Например, площта на квадрата е 49, тогава на каква е страната, равна на?
49 \u003d (а) във втора степен. Решение: a \u003d корен от 49 \u003d 7. Отговор: 7.

Ако трябва да намерите страната на квадратния квадрат, чийто площ е твърде дълга, тогава използвайте калкулатора. Първо наберете номера на зоната и след това натиснете коренния знак на клавиатурата на калкулатора. Полученият номер ще бъде отговорът.

Как да намеря квадратен диагонал, ако площта му е известна?

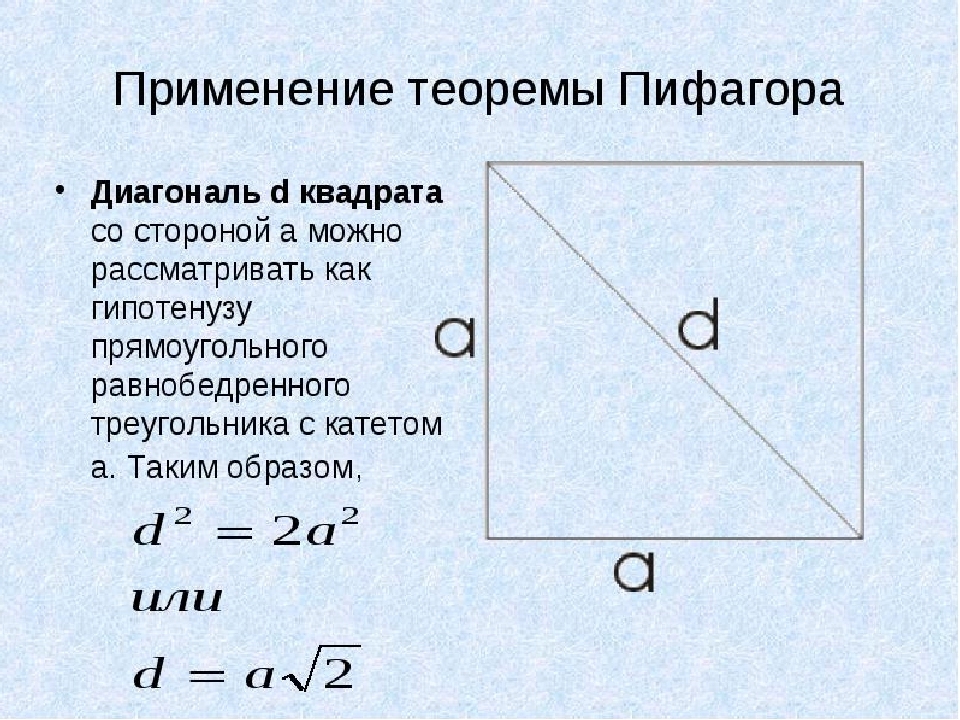
В този пример ще използваме теоремата на Питагор. На квадрат всички страни са равни, а диагоналът д. Ще разгледаме като хипотенуза на правоъгълен триъгълник с крак с крак a. Сега намираме квадратен диагонал, ако е известна неговата площ:

За да не рисуваме цялата питагорска теорема, ще вземем решение за втория вариант: d \u003d aising, където a е страната на квадрата.
И така, ние знаем площта на квадрата, например, тя е равна на 64. Така че едната страна a \u003d √64 \u003d 8.
Оказва се D \u003d 8√2. Коренът на 2 не се оказва целия номер, така че в отговора можете да напишете по този начин: d \u003d 8√2. Но ако искате да изчислите стойността, тогава използвайте калкулатора: √2 \u003d 1.41421356237 и умножете по 8, се оказва 11, 3137084.

Важно: Обикновено в математиката не се оставят числа с голям брой числа в отговор. Необходимо е да се закръгляте или да напуснете с корена. Следователно отговорът на диагонала е, ако площта е 64, както следва: d \u003d 8√2.

Как да намерите квадратна зона през диагонал?

Формулата за намиране на квадратната зона през диагонала е проста:

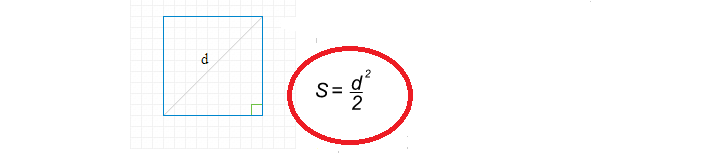
Сега нека напишем решение, за да намерим квадратната област чрез диагонала:

Диагонал D \u003d 8.
8 на площада е 64.
64 Разделете с 2 равни 32.
Квадратната зона е 32.

Съвет: Тази задача има друго решение чрез теоремата на Питагор, но е по -сложна. Затова използвайте решението, което разгледахме.

Как да намеря квадратна зона, знаейки периметъра му?

Периметърът на квадратния квадрат П. - Това е сумата на всички страни. За да намерите неговата зона, знаейки периметъра му, първо трябва да изчислите страната на квадратния квадрат. Решение:

Да предположим, че периметърът е 24. Разделете 24 на 4 страни, оказва се 6 - това е едната страна.
Сега използваме формулата за намиране на зоната, знаейки каква е страната на квадратния квадрат, равна на: S \u003d a в квадрат, s \u003d 6 в квадрат \u003d 36.
Отговор: 36

Както можете да видите, познавайки периметъра на площада, просто намерете неговата зона.

Как да намерите площ от квадрат, вписан в кръг с даден радиус?

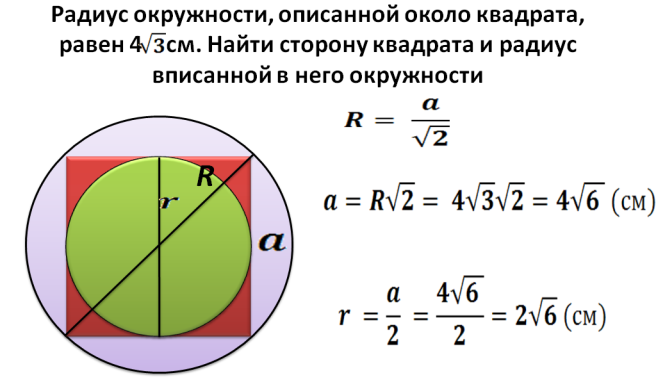
Радиус R - Това е половината диагонал на квадрат, вписан в кръг. Сега можем да намерим диагонал по формулата: d \u003d 2*r. След това намираме квадрата на квадрата, вписан в кръг с даден радиус:

Диагоналът е 2 умножен по радиуса. Например, радиусът е 5, след това диагоналът е равен 2*5=10.
Беше описано по -горе как да се намери квадратът на квадрата, ако е известен диагоналът: S \u003d диагонал в квадрат, разделен на 2. S \u003d 10*10 и се разделя на 2 \u003d 50.
Отговор - 50.

Тази задача е малко по -сложна, но също така лесно се решава, ако знаете всички формули.

Как да намерите площ от квадрат, описан близо до кръг с даден радиус?

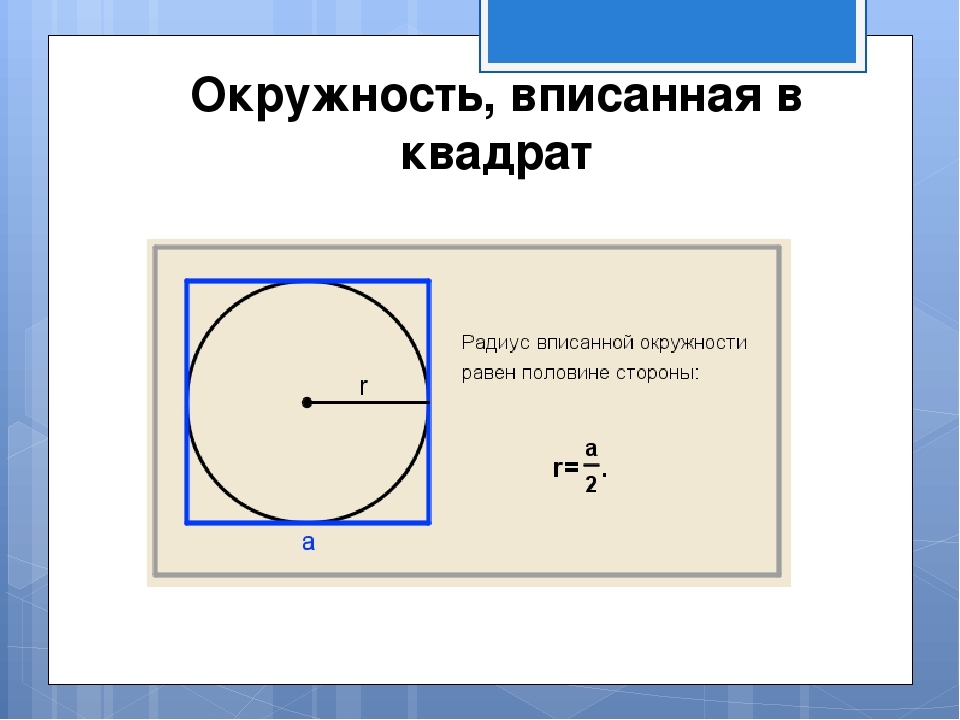
Картината показва, че радиусът на надписания кръг е равен на половината от страната. Страната е разположена според обратната формула, изобразена на снимката: a \u003d 2*r. След това откриваме площта на квадрата, описана близо до кръга с даден радиус съгласно формулата S \u003d и в квадрат. Решение:

Да предположим, че радиусът е 7. Страната на квадрата А е 2*7 \u003d 14.
S \u003d 14 в квадрат \u003d 196.

Ако разбирате същността на решаването на подобни проблеми, тогава можете да ги разрешите бързо и просто. Нека разгледаме още няколко примера.

Примери за решаване на проблеми по темата „квадратна площад“

За да се фиксира покритият материал и да запомните всички формули, е необходимо да се решат няколко примера на проблеми по темата за „квадратна зона“. Започваме с проста задача и преминаваме към решаване на по -сложни: