Как найти площадь квадрата, если известен периметр, диагональ? Как найти найти площадь квадрата вписанного в окружность и описанного около окружности: формула, примеры решения задач. Как найти сторону и диагональ квадрата, если известна его площадь?

Читайте статью, чтобы знать, как находить площадь квадрата разными способами.

Квадрат — это равносторонний прямоугольник. У данного правильного и плоского четырехугольника равенство во всех сторонах, углах и диагоналях. Из-за того что существует такое равенство, формула для вычисления площади и других характеристик, немного видоизменяется по сравнению с иными математическими фигурами. Но это не делает задачи слишком сложными. Давайте разберем все формулы и решения задач в этой статье.

Как найти сторону квадрата, зная его площадь?

Площадь S прямого и квадратного угольников вычисляется по формуле: a умножить на b. Но так как у квадрата полное равенство сторон, то его площадь будет равна: S=(a) во второй степени.  Как узнать величину стороны квадрата, зная его площадь?

• Если известна площадь квадратного угольника, то сторону находим путем исчисления площади из-под квадратного корня.
• К примеру, площадь угольника равна 49, то чему равняется сторона?
• 49=(а) во второй степени. Решение: а=корень из 49=7. Ответ: 7.

Если нужно найти сторону квадратного угольника, площадь которого состоит слишком длинного числа, тогда воспользуйтесь калькулятором. Наберите сначала число площади, а потом нажмите знак корня на клавиатуре калькулятора. Получившееся число и будет ответом.

Как найти диагональ квадрата, если известна его площадь?

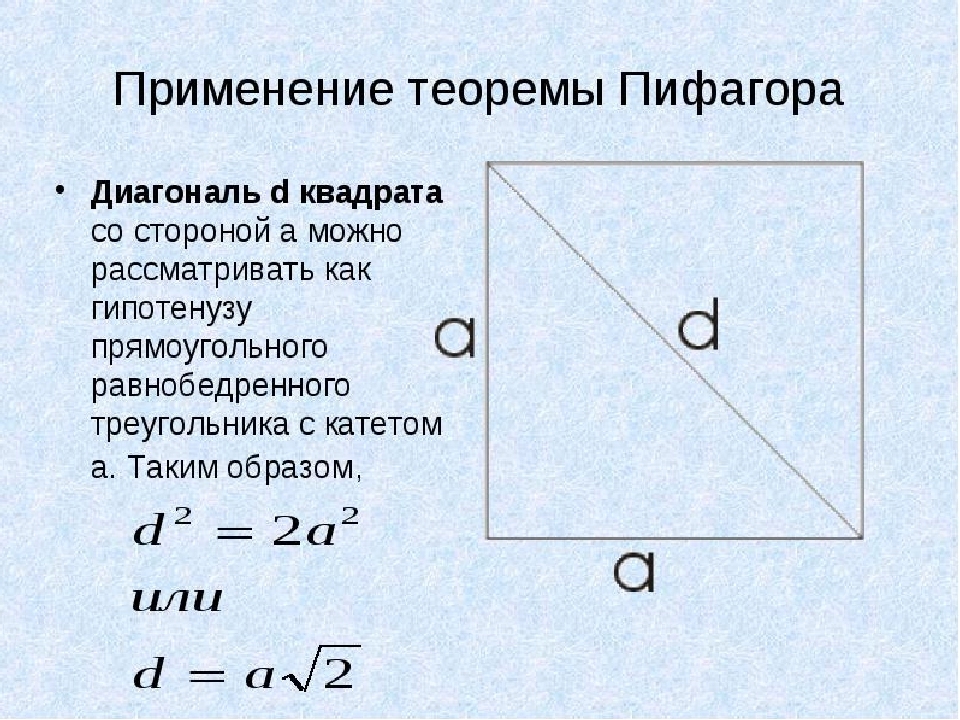
В этом примере будем использовать теорему Пифагора. У квадрата все стороны равны, а диагональ d мы будем рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Теперь находим диагональ квадрата, если известна его площадь:

• Чтобы не расписывать всю теорему Пифагора будем решать по второму варианту: d=a√2, где а — это сторона квадрата. 
• Итак, нам известна площадь квадрата, например, она равна 64. Значит одна сторона а=√64=8.
• Получается d=8√2. Корень из 2 не получается целым числом, поэтому в ответе можно написать именно так: d=8√2. Но, если хочется вычислить значение, тогда воспользуйтесь калькулятором: √2= 1,41421356237 и умножьте на 8, получается 11, 3137084.

Важно: Обычно в математике не оставляют в ответе цифры с большим количеством чисел после запятой. Нужно округлять или оставить с корнем. Поэтому ответ на нахождение диагонали, если площадь равна 64 будет таким: d=8√2.

Как найти площадь квадрата через диагональ?

Формула нахождения площади квадрата через диагональ простая:

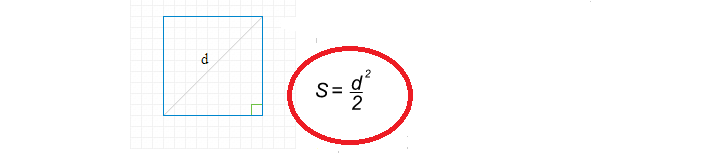
Теперь напишем решение по нахождению площади квадрата через диагональ:

• Диагональ d=8.
• 8 в квадрате равняется 64.
• 64 разделить на 2 равно 32.
• Площадь квадрата равна 32.

Совет: У этой задачи есть еще одно решение через теорему Пифагора, но оно более сложное. Поэтому используйте решение, которое мы рассмотрели.

Как найти площадь квадрата, зная его периметр?

Периметр квадратного угольника P — это сумма всех сторон. Чтобы найти его площадь, зная его периметр, нужно сначала вычислить сторону квадратного угольника. Решение:

• Допустим периметр равен 24. Делим 24 на 4 стороны, получается 6 — это одна сторона.
• Теперь используем формулу нахождения площади, зная чему равна сторона квадратного угольника: S=а в квадрате, S=6 в квадрате=36.
• Ответ: 36

Как видите, зная периметр квадрата, просто найти его площадь.

Как найти площадь квадрата вписанного в окружность с заданным радиусом?

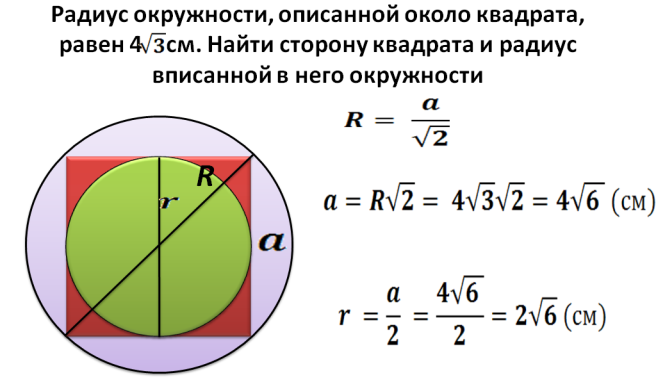
Радиус R — это половина диагонали квадрата, вписанного в окружность. Теперь можем найти диагональ по формуле: d=2*R. Далее находим площадь квадрата вписанного в окружность с заданным радиусом:

• Диагональ равна 2 умножить на радиус. Например радиус равен 5, тогда диагональ равна 2*5=10.
• Выше было описано, как находить площадь квадрата, если известна диагональ: S=диагональ в квадрате разделить на 2. S=10*10 и разделить на 2=50.
• Ответ — 50.

Эта задача немного сложнее, но тоже легко решаемая, если знать все формулы.

Как найти площадь квадрата описанного около окружности с заданным радиусом?

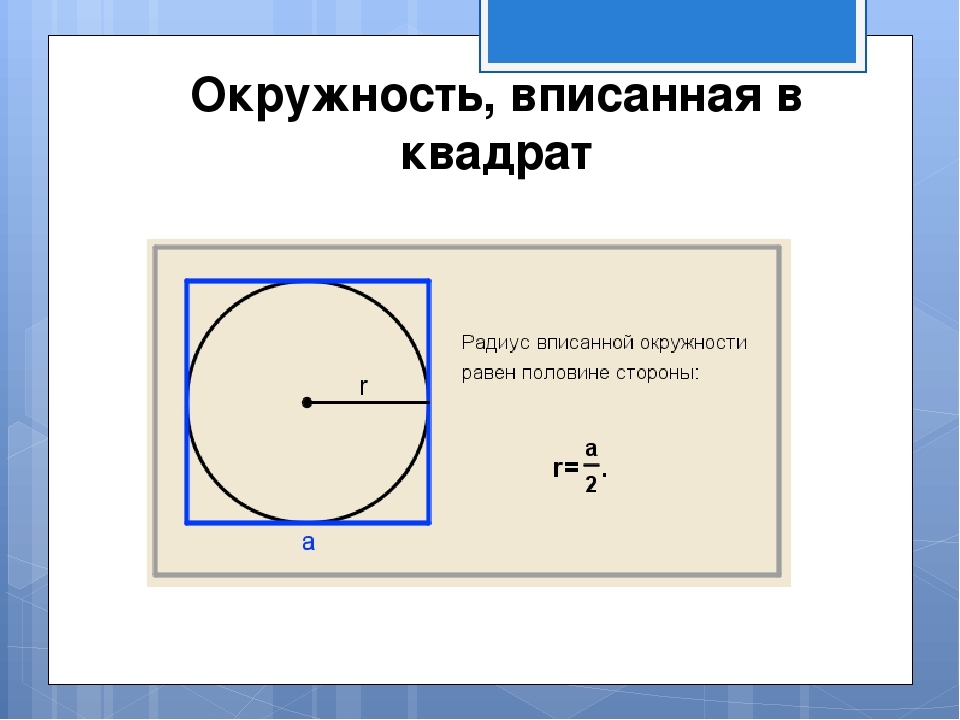
На картинке видно, что радиус вписанной окружности равен половине стороны. Сторона находится по формуле обратной той, которая изображена на картинке: а=2*r. Потом уже находим площадь квадрата описанного около окружности с заданным радиусом по формуле S=а в квадрате. Решение:

• Допустим, радиус равен 7. Сторона квадрата а равна 2*7=14.
• S=14 в квадрате=196.

Если понять суть решения подобных задач, то можно решать их быстро и просто. Давайте рассмотрим еще несколько примеров.

Примеры решения задач на тему «Площадь квадрата»

Чтобы закрепить пройденный материал и запомнить все формулы, необходимо решить несколько примеров задач на тему «Площадь квадрата». Начинаем с простой задачи и движемся к решению более сложных:

Теперь вы знаете, как пользоваться формулой площади квадрата, а значит, вам любая задача под силу. Успехов в дальнейшем обучении!

Видео: Вычисление площади квадрата