Как да изчислим площта на ромбите?

В тази статия ще научите как да намерите областта на ромбите с различни методи. Благодарение на тези формули, тя лесно ще бъде решена чрез проблеми с геометрията, тъй като тук статията ще опише как да се изчисли областта на ромбите, като знае размера на диагонала на по -големия и долния, страничния и диаметъра на надписания кръг в ромб.

Можете да разберете района на ромбския по различни формули. Достатъчно е да знаете свойствата на тази фигура и свойствата на други фигури, тъй като ромбът може да бъде разделен на триъгълници, той може да бъде приравнен с паралелограм и т.н. По -долу ще видите такива формули. Също така трябва да знаете как се различават ромбът и паралелограм. Според математическото определение. Ромбът е фигура на такъв паралелограм с равни страни, но за разлика от квадрата - ромбът няма прави ъгли. Но сумата от двата ъгъла в основата на ромбът ще бъде 180 градуса. Всички тези знания ще бъдат полезни за изчисляване на областта на ромб, след това по -подробно.

Как да изчислим областта на ромб - свойствата на фигурата

Преди да изчислите областта на ромбът, по -добре е да се запознаете със свойствата на тази фигура. Всъщност, благодарение на познаването на тези характеристики, ще бъде по -лесно да се докаже вероятността от определена формула. По -рано вече беше споменато какво е ромб. Това е фигура с равна на всички страни, равна на противоположни остри и тъпи ъгли, но не и права.

Ромбът има следните свойства:

• всички страни са равни една на друга
• ъглите, лежащи един срещу друг, също са равни
• диагоналите на тази фигура са бисектори, в точката на пресичане са разделени на равни сегменти
• диагоналите също се пресичат в центъра на ромбите и под прав ъгъл
• обратните страни на фигурите не могат да се пресичат, дори и да удължите лъчите, те са успоредни, като паралелограм.

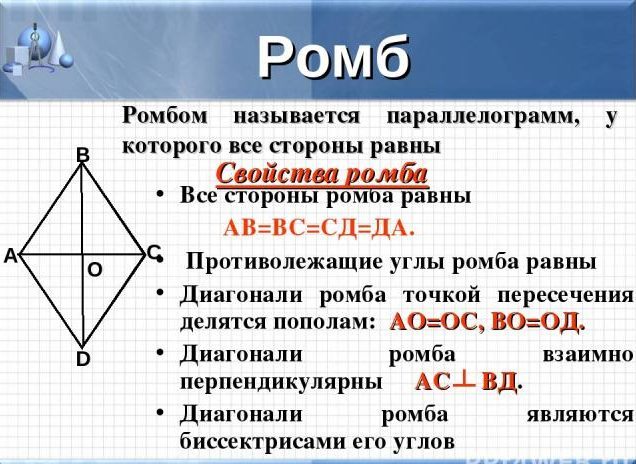
Важно: Моля, обърнете внимание, че ромбът може да бъде разделен на четири правоъгълни триъгълника, които ще бъдат равни на площ или по два равнилни идентични триъгълника, вижте изображението по -горе.

Как да изчислим площта на ромбите?

И така, нека разберем как се изчислява района на ромб. Нека се възползваме от формулата за областта на правоъгълника, където:

• S \u003d a • bкъдето a, b са страните на правоъгълника.

Така че е ясно как да премахнете формулата на зоната на ромбите от тази формула, вижте обяснение:

1. Начертайте ромб, направете височина до основата на BH Rhombus.
2. От точка D до рекламната линия, също изчертайте височина на CH1.
3. Оказва се, че триъгълникът ABH и триъгълникът CH1D са равни един на друг на две общи страни, ∠ ∠ ∠ at в капака между тях.
4. Така че AH \u003d DH1. Площта на получения квадрат ще бъде равна на площта на ромб
5. Така че BH • HH1 - Това е зоната на ромбите, с други думи, работата на BH Rhombus отстрани на AD и ще бъде S област на ромб, тъй като HH1 \u003d BC, а Bh е The височина.

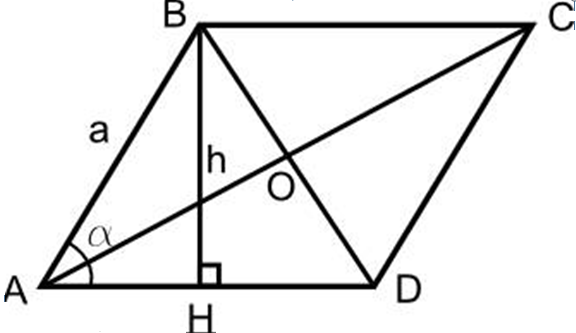
Следва от доказателството, че:

• S rombus \u003d a • h и измерени в квадратни единици.

Как да намерите зоната на ромбите, познавайки ъгъла и страната на геометричната фигура?

Сега знаем как изглежда формулата на зоната на ромб, можем да намерим зона на Ромба на същата формула, като знаем каква е страната на ромбите е равна на страната на ромб, например, остра в основата, както в снимката по -долу.

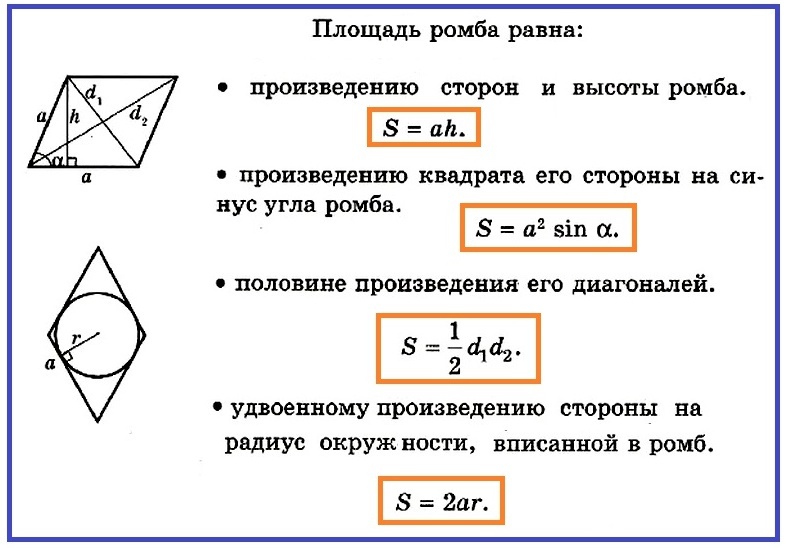
• S \u003d a • h

Но в нашия случай ние сме непознати за височината на ромбите, трябва да се намери. За да направите това, ще трябва да помислите за правоъгълен триъгълник, който се оказа, когато височината е изтеглена към основата на ромбите.

В този триъгълник е известен хипотенуза и ∠α. За да изчислите площта на цялата фигура, ще трябва да намерите височина. НО h \u003d a • грех те. Така е площта на равностранен паралелограм (ромб) е:

• S \u003d A • A • SIN Те AX \u003d A² • Sinown.

Как да изчислим областта на ромб, знаейки нейните диагонали?

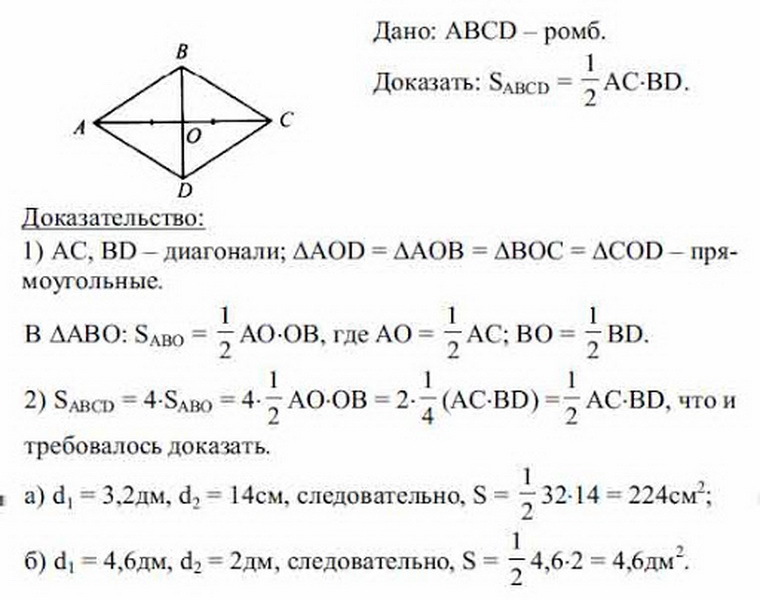
За да се разбере формулата на областта на ромбите, когато са известни само (a, b) диагонали, трябва да се вземе предвид следният пример. BCDA е даден - ромб и знайте какви са равни диагоналите. Сега е необходимо да се намери S зона на равностранна паралелограма по отношение на диагоналите.

Преди това бяха разгледани свойствата на ромбите. Диагоналите на ромбите са равни, в точката на пресичане те са разделени на равни сегменти. От това следва, че всички триъгълници, които са изписани на фигурата в резултат на пресечната точка на двата диагонала, също са равни един на друг и те са правоъгълни (от три страни). За да намерите площта на ромб, е достатъчно да намерите площта на един триъгълник и да умножите данните, получени по 4.

Общо се оказва, че:

• S Rhombus \u003d 4 (1/2 AO • OB + 1/2 BO • OC + 1/2 OC • OD + 1/2 OD • AO) \u003d 4 • 1/8 AC • BD \u003d 1/2 BD • AC, Общият квадрат s romm ще бъде \u003d работа a • b (диагонали), разделен на две: S \u003d 1/2 a • b

Как да изчислим площта на ромб, познавайки неговата страна и радиуса на кръга, вписан в него?

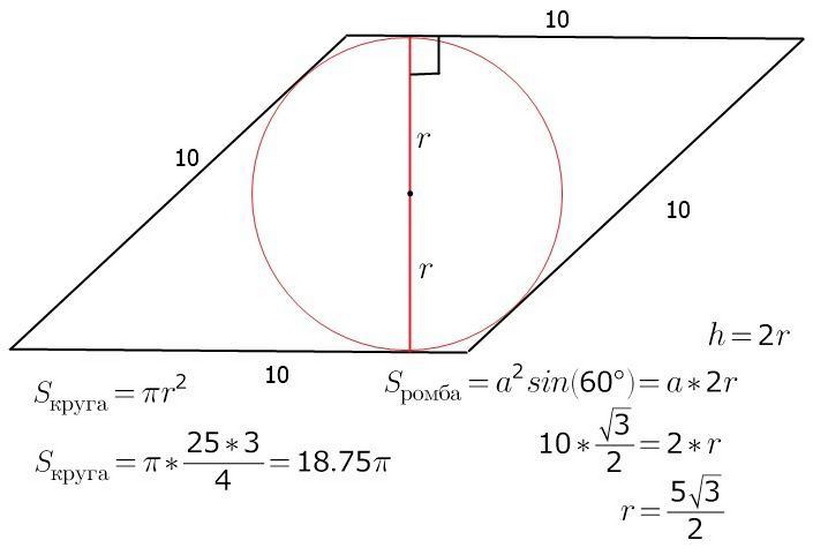
Площта на ромбът може да бъде изчислена, като се знае R - радиус и A - дължината на страната на фигурата. Вече е известно, че S - площта на фигурата ще бъде равна на работата b - отстрани на h - височина. През центъра на кръга той ще бъде и центърът за кръстовище A, B е диагоналите на ромбите. Извършете височината и в същото време диаметърът на ромбите. Изображението показва, че височината на фигурата е два радиуси на кръга. Сега ще бъде лесно да се намери района на самия ромб:

• S \u003d a • h \u003d a • 2r

По -долу вижте примера на задачата по тази тема.

Все още вижте такива статии по тази тема тук:

1. Площта на правоъгълника, как да намеря?
2. Как да намеря зона за кръг?
3. Квадратна зона - формули.

Видео: Пример за това как да се изчисли площта на ромбите